Day of experiment: Tuesday
Date of experiment: 20/5/2014
Experiment: Determination of diffusion coefficient
Objectives:
To determine the value of diffusion coefficient
Introduction:
Diffusion describes the spread of particles through random motion from regions of higher concentration to regions of lower concentration. The time dependence of the statistical distribution in space is given by the diffusion equation. Fick's laws of diffusion describe diffusion and can be used to solve for the D. The diffusion coefficient (D) is the amount of a particular substance that diffuses across a unit area in 1 s under the influence of a gradient of one unit. It is usually expressed in the
units . It can be expressed in dm = -DA(dc/dx)dt (i).
Diffusion coefficient depends on size and shape of molecule, interaction with solvent and viscosity of solvent. If a solution which have neutral molecules with concentration, Mo, put in a slim tube next to a water tube, diffusion can be stated as
M = M0 exp(-x²/ 4 Dt) ……… ()
where M is the concentration at x distance from the level between water and solution that measured at time t.
By changing equation () to logarithmic form, we can obtain
ln M = (ln M0 -x²/4Dt) or 2.303 x 4D (log 10 M0 –log 10 M) t = x² ……… ()
Thus, one x² versus t graph can produce a straight line which cross the origin with its gradient 2.303 x 4D (log 10 M0–log 10 M). From here, D can be counted.
If the molecules in the solution are assumed to be a sphere shape, then the size and mass of the molecules can be counted from Stokes-Einstein equation.
D = kT/6пŋa ……… ()
(D =kT/9 and 9 = 6пŋa )
where k is the Boltzmann constant 1.38 x 1023 Jk-1 , T is the temperature in Kelvin, ŋ is the viscosity of the solute, in Nm-2s and a half diameter of molecule in M. The volume for that certain sphere molecule is 4/3пa³, thus the mass of M is equal to 4/3пa³ρ (ρ = the density of the molecule).
As we know that the molecular mass of M = mN (N is the Avogadro’s number 6.02 x 1023mol-1 ).
M = 4/3лa³Nρ ……… ()
Diffusion for molecules with charges, equation () has to be changed to insert the gradient force effect that exists between the solution and the solvent. However, this can be overcome by adding a little of sodium chloride into the solvent to prevent the forming of this gradient force.
Agar gel is a semi-solid that can be interfered by water molecules. The water moleculesform a continuous phase in the agar gel. As such, the solute molecules can be diffused freely in the water. Thus, these agar gels provide a supportive system that can be used in the experiment for diffusion of certain molecules in a aqueous medium.
Materials : Apparatus :
Agar powder 500 mL beaker
Ringer solution 5 mL pipette
1 : 500.000 crystal violet solution Glass rod
1 : 200 crystal violet solution 14 test tubes with covers
1 : 400 crystal violet solution Hot plate
1 : 600 crystal violet solution
1 : 500,000 bromothymol blue solution
1 : 200 bromothymol blue solution
1 : 400 bromothymol blue solution
1 : 600 bromothymol blue solution
Procedures:
1)
7g of agar powder was weighed and mixed with 420ml of Ringer solution.
2)
The mixture in step 1 was stirred and boiled on a hot plate until transparent yellowish solution.
3)
20ml of the agar solution was pour into each 6 test tubes. The test tubes ware put in the fridge to let them cool.
4)
An agar test tube which contained 5ml of 1:500,000 crystal violet was being prepared for standardize the color distance that cause by the diffusion of crystal violet.
5)
After the agar solutions in the test tubes were become solidify, 5ml of 1:200, 1:400, 1:600 crystal violet solution were pour into each test tubes and 3 test tubes were to be put in room temperature while another 3 were been put in 37ºc water bath.
6)
The test tubes were been closed immediately to prevent the vaporization of the solutions.
7)
Step 2 to 6 was repeated for Bromothymol Blue solutions.
8)
The data of the distance of solute diffusion was recorded and graph x² versus time was been plotted.
Results:
System (370C)
|
Time (hr)
|
X (m)
|
()
|
Slope of Graph
(m²hrˉ¹)
|
D (m²hrˉ¹)
|
Temperature
(ºc)
|
Average
of Diffusion Coefficient (m²hrˉ¹)
|
Crystal Violet with dilution 1:200
|
0
20
44
68
140
164
188
212
|
0.032
0.041
0.049
0.058
0.071
0.077
0.082
0.094
|
0.001024
0.001681
0.002401
0.003364
0.005041
0.005929
0.006724
0.008836
|
2.1
|
6.71x10-7
|
37
|
9.70x10-7
|
Crystal Violet with dilution 1:400
|
0
20
44
68
140
164
188
212
|
0.042
0.046
0.050
0.055
0.070
0.078
0.085
0.091
|
0.001764
0.002116
0.002500
0.003025
0.004900
0.006084
0.007225
0.008281
|
3.0
|
1.05x10-6
|
37
| |
Crystal Violet with dilution 1:600
|
0
20
44
68
140
164
188
212
|
0.073
0.076
0.078
0.080
0.090
0.096
0.097
0.098
|
0.005329
0.005776
0.006084
0.006400
0.008100
0.009216
0.009409
0.009604
|
3.2
|
1.19x10-6
|
37
|
System (370C)
|
Time (hr)
|
X (m)
|
()
|
Slope of Graph
(m²hrˉ¹)
|
D (m²hrˉ¹)
|
Temperature
(ºc)
|
Average
of Diffusion Coefficient (m²hrˉ¹)
|
Bromothymolblue with dilution
1:200
|
0
20
44
68
140
164
188
212
|
0.018
0.021
0.057
0.068
0.081
0.085
0.091
0.098
|
0.000324
0.000441
0.003249
0.004624
0.006561
0.007225
0.008281
0.009604
|
4.2
|
1.34x10-6
|
37
|
3.36x10-6
|
Bromothymolblue with
dilution
1:400
|
0
20
44
68
140
164
188
212
|
0.040
0.045
0.050
0.056
0.074
0.080
0.087
0.095
|
0.001600
0.002025
0.002500
0.003136
0.005476
0.006400
0.007569
0.009025
|
3.3
|
1.16x10-6
|
37
| |
Bromothymolblue with
dilution
1:600
|
0
20
44
68
140
164
188
212
|
0.062
0.063
0.065
0.070
0.080
0.084
0.090
0.093
|
0.003844
0.003969
0.004225
0.004900
0.006400
0.007056
0.008100
0.008649
|
2.3
|
8.55x10-7
|
37
|
System (Room temperature)
|
Time (hr)
|
X (m)
|
()
|
Slope of Graph
(m²hrˉ¹)
|
D (m²hrˉ¹)
|
Temperature
(ºc)
|
Average
of Diffusion Coefficient (m²hrˉ¹)
|
Crystal Violet with dilution 1:200
|
0
20
44
68
140
164
188
212
|
0.031
0.038
0.045
0.050
0.072
0.076
0.080
0.085
|
0.000961
0.001444
0.002025
0.002500
0.005184
0.005776
0.006400
0.007225
|
3.0
|
9.58x10-7
|
28
|
6.87x10-7
|
Crystal Violet with dilution 1:400
|
0
20
44
68
140
164
188
212
|
0.060
0.066
0.070
0.075
0.085
0.087
0.090
0.093
|
0.003600
0.004356
0.004900
0.005625
0.007225
0.007569
0.008100
0.008649
|
2.3
|
8.06x10-7
|
28
| |
Crystal Violet with dilution 1:600
|
0
20
44
68
140
164
188
212
|
0.060
0.062
0.064
0.065
0.069
0.071
0.073
0.074
|
0.003600
0.003844
0.004096
0.004225
0.004761
0.005041
0.005329
0.005476
|
8.0
|
2.97x10-7
|
28
|
System (Room temperature)
|
Time (hr)
|
X (m)
|
()
|
Slope of Graph
(m²hrˉ¹)
|
D (m²hrˉ¹)
|
Temperature
(ºc)
|
Average
of Diffusion Coefficient (m²hrˉ¹)
|
Bromothymolblue with dilution
1:200
|
0
20
44
68
140
164
188
212
|
0.025
0.028
0.032
0.040
0.048
0.060
0.065
0.068
|
0.000625
0.000784
0.001024
0.001600
0.002304
0.003600
0.004225
0.004624
|
1.9
|
6.07x10-7
|
28
|
1.824x10-6
|
Bromothymolblue with
dilution
1:400
|
0
20
44
68
140
164
188
212
|
0.040
0.048
0.052
0.058
0.070
0.072
0.075
0.082
|
0.001600
0.002304
0.002704
0.003364
0.004900
0.005184
0.005625
0.006724
|
2.2
|
7.71x10-7
|
28
| |
Bromothymolblue with
dilution
1:600
|
0
20
44
68
140
164
188
212
|
0.071
0.074
0.077
0.079
0.084
0.086
0.087
0.089
|
0.005041
0.005476
0.005929
0.006241
0.007056
0.007396
0.007569
0.007921
|
1.2
|
4.46x10-7
|
28
|
Bromothymol blue at 28ºC
Calculation:
1.
Crystal Violet system with dilution 1:200 at 37ºC :
From graph, gradient
= 2.1x10-5 m²hr-1
Mo=1:200 M=1:500,000 (standard)
=1/200 =1/500,000
=5x10-3 =2x10-6
2.303 x 4D (log 10 Mo – log 10 M) = 2.1x10-5 m²hr-1
2.303x4D [log 10 (5x10-3 )-log 10 (2x10-6 )] = 2.1x10-5 m²hr-1
Hence, D = 6.71x10-7 m²hr-1
2.
Crystal Violet system with dilution 1:400 at 37ºC :
From graph, gradient
=3.0x10-5 m²hr-1
Mo=1:400 M=1:500,000 (standard)
=1/400 =1/500,000
=2.5x10-3 =2x10-6
2.303 x 4D (log 10 Mo – log 10 M) = 3.0x10-5 m²hr-1
2.303x4D [log 10 (2.5x10-3 )-log 10 (2x10-6 )] = 3.0 x10-5 m²hr-1
Hence, D = 1.05x10-6 m²hr-1
3.
Crystal Violet system with dilution 1:600 at 37ºC :
From graph, gradient
= 3.2x10-5 m²hr-1
Mo=1:600 M=1:500,000 (standard)
=1/600 =1/500,000
=1.67x10-3 =2x10-6
2.303 x 4D (log 10 Mo – log 10 M) = 3.2x10-5 m²hr-1
2.303x4D [log 10 (1.67x10-3 )-log 10 (2x10-6 )] = 3.2x10-5 m²hr-1
Hence, D = 1.19x10-6 m²hr-1
4.
Average diffusion coefficient, m²hr-1 for Crystal Violet system at 37ºC
=[(6.71x10-7 m²hr-1 ) + (1.05x10-6 m²hr-1) + (1.19x10-6 m²hr-1)]/3
=9.70x10-7 m²hr-1
5.
Bromothymol Blue system with dilution 1:200 at 37ºC :
From graph, gradient
=4.2x10-5 m²hr-1
Mo=1:200 M=1:500,000 (standard)
=1/200 =1/500,000
=5x10-3 =2x10-6
2.303 x 4D (log 10 Mo – log 10 M) = 4.2x10-5 m²hr-1
2.303x4D [log 10 (5x10-3 )-log 10 (2x10-6 )] = 4.2x10-5 m²hr-1
Hence, D = 1.34x10-6 m²hr-1
6.
Bromothymol Blue system with dilution 1:400 at 37ºC :
From graph, gradient
= 3.3x10-5 m²hr-1
Mo=1:400 M=1:500,000 (standard)
=1/400 =1/500,000
=2.5x10-3 =2x10-6
2.303 x 4D (log 10 Mo – log 10 M) = 3.3x10-5 m²hr-1
2.303x4D [log 10 (2.5x10-3 )-log 10 (2x10-6 )] = 3.3x10-5 m²hr-1
Hence, D = 1.16x10-6 m²hr-1
7.
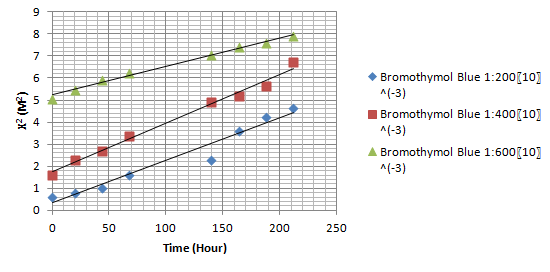
Bromothymol Blue system with dilution 1:600 at 37ºC :
From graph, gradient
= (8.40-1.50) x 10-4 / (150-27)m²hr-1
= 2.3x10-5 m²hr-1
Mo=1:600 M=1:500,000 (standard)
=1/600 =1/500,000
=1.67x10-3 =2x10-6
2.303 x 4D (log 10 Mo – log 10 M) = 2.3x10-5 m²hr-1
2.303x4D [log 10 (1.67x10-3 )-log 10 (2x10-6 )] = 2.3x10-5 m²hr-1
Hence, D = 8.55x10-7 m²hr-1
8.
Average diffusion coefficient, m²hr-1 for Bromothymol Blue system at 37ºC
=[(1.34x10-6 m²hr-1 ) + (1.16x10-6 m²hr-1) + (8.55x10-7 m²hr-1)]/3
=3.36x10-6 m²hr-1
9.
Crystal Violet system with dilution 1:200 at 28ºC :
From graph, gradient
=3.00x10-5 m²hr-1
Mo=1:200 M=1:500,000 (standard)
=1/200 =1/500,000
=5x10-3 =2x10-6
2.303 x 4D (log 10 Mo – log 10 M) = 3.00x10-5 m²hr-1
2.303x4D [log 10 (5x10-3 )-log 10 (2x10-6 )] = 3.00x10-5 m²hr-1
Hence, D = 9.58x10-7 m²hr-1
10.
Crystal Violet system with dilution 1:400 at 28ºC :
From graph, gradient
=2.30x10-5 m²hr-1
Mo=1:400 M=1:500,000 (standard)
=1/400 =1/500,000
=2.5x10-3 =2x10-6
2.303 x 4D (log 10 Mo – log 10 M) = 2.30x10-5 m²hr-1
2.303x4D [log 10 (2.5x10-3 )-log 10 (2x10-6 )] = 2.30x10-5 m²hr-1
Hence, D = 8.06x10-7 m²hr-1
11.
Crystal Violet system with dilution 1:600 at 28ºC :
From graph, gradient
=8.00x10-6 m²hr-1
Mo=1:600 M=1:500,000 (standard)
=1/600 =1/500,000
=1.67x10-3 =2x10-6
2.303 x 4D (log 10 Mo – log 10 M) = 8.00x10-6 m²hr-1
2.303x4D [log 10 (1.67x10-3 )-log 10 (2x10-6 )] = 8.00x10-6 m²hr-1
Hence, D = 2.97x10-7 m²hr-1
12.
Average diffusion coefficient, m²hr-1 for Crystal Violet system at 28ºC
= [(9.58x10-7 m²hr-1) + (8.06x10-7 m²hr-1) + (2.97x10-7 m²hr-1)]/3
= 6.87x10-7 m²hr-1
13.
Bromothymol Blue system with dilution 1:200 at 28ºC :
From graph, gradient
=1.90x10-5 m²hr-1
Mo=1:200 M=1:500,000 (standard)
=1/200 =1/500,000
=5x10-3 =2x10-6
2.303 x 4D (log 10 Mo – log 10 M) = 1.90x10-5 m²hr-1
2.303x4D [log 10 (5x10-3 )-log 10 (2x10-6 )] = 1.90x10-5 m²hr-1
Hence, D = 6.07x10-7 m²hr-1
14.
Bromothymol Blue system with dilution 1:400 at 28ºC :
From graph, gradient
= 2.20x10-5 m²hr-1
Mo=1:400 M=1:500,000 (standard)
=1/400 =1/500,000
=2.5x10-3 =2x10-6
2.303 x 4D (log 10 Mo – log 10 M) = 2.20x10-5 m²hr-1
2.303x4D [log 10 (2.5x10-3 )-log 10 (2x10-6 )] = 2.20x10-5 m²hr-1
Hence, D = 7.71x10-7 m²hr-1
15.
Bromothymol Blue system with dilution 1:600 at 28ºC :
From graph, gradient
=1.2x10-5 m²hr-1
Mo=1:600 M=1:500,000 (standard)
=1/600 =1/500,000
=1.67x10-3 =2x10-6
2.303 x 4D (log 10 Mo – log 10 M) = 1.2x10-5 m²hr-1
2.303x4D [log 10 (1.67x10-3 )-log 10 (2x10-6 )] = 1.2x10-5 m²hr-1
Hence, D = 4.46x10-7 m²hr-1
16.
Average diffusion coefficient, m²hr-1 for Bromothymol Blue system at 28ºC
=[(6.07x10-7 m²hr-1 ) + (7.71x10-7 m²hr-1) + (4.46x10-7 m²hr-1)]/3
=1.824x10-6 m²hr-1
Questions:
1) From the experiment value for D28, the value of D37
using the following equation are:
D28oC/ D37oC
= T28oC/ T37oC
A) Crystal violet
i.
1:200
(9.58
x 10-5m2/hour)/ D37oC = 28/37
Experimental value
= 6.71 x 10-7
of D37oC
ii.
1:400
(2.3
x 10-5m2/hour)/ D37oC = 28/37
D37oC = 3.039x 10-5 m2/hour
Experimental value
of D37oC
iii.
1:600
(8.00
x 10-6m2/hour)/ D37oC = 28/37
Experimental value
of D37oC
Average D28ºC =
6.87x10-7 m²hr-1
D28ºC / D37ºC = T28ºC/T37ºC
6.87x10-7 m²hr-1 /
D37ºC = 28 / 37
D37ºC = 9.078x10-7 m²hr-1
Experimental value of D37ºC =
9.7 x 10-7 m²hr-1
The
D37ºC value is 9.078x10-7 m²hr-1 while the
experimental value is 9.7x10-7 m²hr-1. There is a
slightly difference between these two values, where it is less of 6.22x10-8 m²hr-1of D37ºC value
from the experimental value.
B) Bromothymol blue
i.
1:200
(6.07
x 10-7m2/hour)/ D37oC = 28/37
Experimental value of
D37oC =
1.34 x 10-6 m2/hour
ii.
1:400
(7.71
x 10-7m2/hour)/ D37oC = 28/37
D37oC
1.019 x 10-6 m2/hour
Experimental value of D37oC = 1.16 x 10-6 m2/hour
iii.
1:600
(4.46
x 10-7m2/hour)/ D37oC = 28/37
D37oC
5.894 x 10-7
m2/hour
Experimental value of D37oC = 8.55 x 10-7 m2/hour
Average D28ºC = 2.824x10-6
m²hr-1
D28ºC / D37ºC = T28ºC/T37ºC
1.824x10-6 / D37ºC =
28 / 37
D37ºC = 2.41x10-6 m²hr-1
Experimental value
of D37ºC =
3.36 x 10-6
m²hr-1
The
D37ºC value is 2.41x10-6 m²hr-1 while the
experimental value is 3.36x10-6 m²hr-1. There is a
slightly difference between these two values, where it is less of 9.5x10-7 m²hr-1of D37ºC value
from the experimental value.
2.Between
Crystal Violet and Bromothymol Blue, which one diffuse much faster? Explain if
there are any differences in these diffusion coefficients.
M = 4/3
πa2Nρ
a3 = 3M/4πNρ
a = cube root M/4πNρ
where:
M = molecular weight,
a = size of particle,
ρ = density,
N = Avogadro’s number 6.023 x 1023
From the formula above, we can say that the size of particle
is proportional to the molecular weight. So, the smaller the size of particle,
the easier the particle to diffuse into the medium.
Based on the formula, the
diffusion coefficient, D is inversely proportional to the molecular weight.
Since crystal violet has a higher diffusion coefficient than that in
bromothymol blue, it diffuse quickly in the agar medium than bromothymol blue.
Besides, the molecular weight of crystal violet is smaller, i.e 407.99 gmol-1
when compared to that in bromothymol blue that is 624.38 gmol-1.
So, it facilitates the diffusion of the particles into the solid agar medium.
Discussion:
In this experiment, some errors had been
done and this caused inaccuracy to the final result. The first error is the
agar that we form are not solid enough. This may be due to some of the agar
powder that was not dissolved completely in the Ringer’s solution while
heating. When the agar powder do not dissolve completely, the agar is difficult
to be formed as it cannot solidify. The result of our experiment is therefore
affected as the bromothymol blue and crystal violet solution can diffuse easily
through the agar. Besides, parallax error may occur due to the difficulty in
determining the colour of 1:600 bromothymol blue and crystal violet solution.
These two dilute solution are very light in colour and when they diffuse
through the agar, it is difficult to determine the actual distance the chemical
solution had diffused. Furthermore, as different students are taking the
readings in turns within the two weeks, the inconsistency of result may arise. For
example the method and standard in measuring the diffusion distance is
different between each students. Hence, there is a high possibility that error
may occur and resulting in inaccurate data. The errors formed can be proved
while plotting the graphs and also while calculating the values using D28oC/
D37oC = T28oC/ T37oC. From the
calculations, it is shown that the values of the calculated D37oC is different from the
experimental data. From the graph, there are many points that the
straight line does not pass through. Since the Crystal Violet particles diffuse
spontaneously, so the x value taken is from personal judgement and estimation. It
varies in different people. Moreover, the room temperate is not kept constant
for the day and night. This will indirectly affect the diffusion coefficient
and also the result of experiment.
Fick’s Law states that the diffusion coefficient is affected
the temperature. For the diffusion coefficient of the liquid, we can use the
Stokes-Einstein equation:
DT1/ DT2 = T1VT2 / T2VT1
where:
T1 and T2
denote temperatures 1 and 2, respectively
D is the diffusion coefficient
(cm²/s)
T is the absolute temperature
(K),
V
is the dynamic viscosity of the solvent (Pa·s)
From
the above equation we can conclude that the diffusion coefficient is directly
proportional to the temperature. The higher the temperature, the higher
the tendency the particles gain energy and collide with each other more vigorously. Therefore, it results in
higher diffusion rate through the agar medium as compared to the one with lower temperature(28 oC ) This can also be shown from
the experiment’s results. In the crystal violet experiment, when we compare the
average diffusion coefficient for 28°C and 37°C, we can see that the diffusion
coefficient for 37°C (9.70x10-7) is higher than 28°C (6.87 x10-7). For the bromothymol blue,
the diffusion coefficient for 37°C (3.36x10-6) is also higher than 28°C (1.824
x10-6).
The rate
of absorption is directly proportional with diffusion coefficient. The
smaller the particle the faster it dissolves. Crystal violet have a smaller
molecular weight compared to bromothymol blue thus it’s supposed to have higher
diffusion coefficient. But based from the result shows that bromothymol blue have
a higher diffusion coefficient and this is due to the error that occur in this
experiment.
The rate of diffusion obeys Fick’s Law of
Diffusion too. It states that the rate of change in concentration of solute
with the time is directly proportional to the concentration difference between
the two sides of diffusion layer. Assuming the solute is moving in x direction,
then the solvent molecules will moving in opposite direction, which is –x
direction. Hence, if concentration of solute is high, this create a net flow of
solute in the x direction. In this
practical, the equation given is:
ln M = ln Mo –x2/4Dt
or 2.303
x 4D (log10 Mo – log10 M) t = x2
M is the system with the dilution 1:500,000. which function
as a standard system during this practical. When Mo is increased, the value
of(log 10 Mo- log 10
M) will increase. This causes the concentration gradient become larger
and thus the driving force that leads to the diffusion would be larger and the
rate of diffusion process will increase. Therefore, when concentration of
solutes increases, the diffusion coefficient increases. Therefore, for both
Crystal Violet and Bromothymol Blue system at 28 ºC and 37ºC, the diffusion is
the fastest in 1:200 system followed by 1:400 and the slowest is 1:600.
For the crystal violet experiment at 37°C, our
data is inaccurate as the diffusivity increases ascendingly form 1:200 to
1:600. However, for the crystal violet experiment at 28°C,we can see that as
the concentration Mo decrease from 1:200, 1:400 and 1:600, the diffusivity
of crystal violet decrease. For the bromothymol blue experiment at 37°C, the
data is considered accurate because as the concentration Mo decrease
from 1:200, 1:400 and 1:600, the diffusivity of bromothymol blue also decreases.
But for the result at 37°C we have found that the diffusion
coefficient for concentration 1:400 is higher than 1:200 when it supposed to be
lower. This may be due to the error during the experiment where the agar is
still not hard enough when we pour the bromothymol blue in test tube 1:400.
This causes the solute to easily diffuse through the agar and produce an
incorrect reading.
Conclusion:
Diffusion coefficient for Crystal Violet system at 28ºC , D28ºC is 6.87x10-7 m²hr-1 while at 37ºC, D37ºC is 9.7x10-7 m²hr-1.The diffusion coefficient for Bromothymol Blue system at 28ºC,D28ºC is 1.824x10-6 m²hr-1while at 37ºC , D37ºC is 3.36x10-6 m²hr-1. The temperature, concentration and molecular mass of diffusing molecules are the main factors affecting the diffusion coefficient.
References:
Patrick J. Sinko, 2006, Martin’s Physical Pharmacy and Pharmaceutical Science 5th Ed. Lippincott Williams and Wilkin.
A.T.Florence and D.Attwood. (1998). Physicochemical Principals of Pharmacy, 3rd Edition. Macmillan Press Ltd.
Michael E. Aulton, 2007, Aulton’s Pharmaceutics’s: The Design and Manufacture of Madicines,Churchill Livingstone Elsevier.